

SEMILLERO SIMAC
Elaborado por Maria Chinchilla Peñaranda
Maira Trespalacio Hernandez
Contenido
I PRE-CALCULO
Ecuaciones (Concepto Y Ejemplo)
Qué es una ecuación?.
Es una igualdad algebraica que se verifica para ciertos valores de la variable.
Con otras palabras:
Es una igualdad en las que aparecen números y letras (llamadas incógnitas o variables) relacionados mediante operaciones matemáticas.
La incógnita de una ecuación es la letra con valor desconocido.
El grado de una ecuación es el mayor exponente con que figura la incógnita en la ecuación una vez realizadas todas las operaciones.
Cuando la ecuación sólo contiene una letra le llamamos ecuaciones con una incógnita.(Habitualmente, la x, pero no necesariamente).
Decimos que las ecuaciones son de primer grado cuando dicha letra no está elevada a ninguna
potencia (el exponente es 1 y puede omitirse).
Ecuaciones Cuadráticas

Una ecuación de segundo grado es una ecuación de tipo ax +
bx + c = 0 e la cual a, b, c, son constante y a = 0, en otras palabras es toda
ecuación en la cual el mayor exponente es 2.
Ecuación en segundo grado completas son ecuaciones
de la forma ax + b +c = 0
Ecuación en segundo grado simples son ecuaciones
de la forma ax +c = 0
Diremos que la incompleta si b o c, o ambas a la
vez son cero.
Diremos que es completa cuando ninguno de los
coeficientes es cero.
Nota:
Las Ecuaciones Cuadráticas se pueden dar por la factorización, Y por ecuación cuadrática
Formula de Ecuación Cuadrática

Ecuaciones de tercer grado
Una ecuación de tercer grado es aquella cuyo grado mayor es 3, pudiéndose reducir al tipo:
ax3 + bx2 + cx + d = 0
donde a, b, c y d son los coeficientes. En principio, estas ecuaciones tienen 3 soluciones, aunque es posible que no todas sean reales.
No existe una forma sencilla para resolver este tipo de ecuaciones, y en muchos casos hay que hacerlo mediante cálculos numéricos, pero sí sabemos resolverlas en el caso de que una de las tres soluciones sea entera, ya que, en este caso, esa solución es un divisor del término independiente, d.
Vamos probando, pues, mediante Ruffini con todos los divisores de d hasta dar con ella. Una vez hallada esta raíz, reducimos la ecuación a una de segundo grado, que ya sabemos resolver, con la que obtenemos las otras dos soluciones.
Una ecuación de tercer grado es aquella cuyo grado mayor es 3, pudiéndose reducir al tipo:
No existe una forma sencilla para resolver este tipo de ecuaciones, y en muchos casos hay que hacerlo mediante cálculos numéricos, pero sí sabemos resolverlas en el caso de que una de las tres soluciones sea entera, ya que, en este caso, esa solución es un divisor del término independiente, d.
Vamos probando, pues, mediante Ruffini con todos los divisores de d hasta dar con ella. Una vez hallada esta raíz, reducimos la ecuación a una de segundo grado, que ya sabemos resolver, con la que obtenemos las otras dos soluciones.
Desigualdad
Una desigualdad expresa que dos valores no son iguales.
a ≠ b expresa que a es diferente de b
Hay otros símbolos especiales que muestran en qué sentido las cosas no son iguales.
a < b dice que a es menor que b
a > b dice que a es mayor que b
(estos dos son conocidos como desigualdades estrictas)
a ≤ b significa que a es menor o igual que b
Una desigualdad expresa que dos valores no son iguales.
a ≠ b expresa que a es diferente de b
Hay otros símbolos especiales que muestran en qué sentido las cosas no son iguales.
a < b dice que a es menor que b
a > b dice que a es mayor que b
(estos dos son conocidos como desigualdades estrictas)
a ≤ b significa que a es menor o igual que b
Una inecuación cuadrática es una inecuación de la forma:
Tipos de intervalos
-intervalo abierto
Es aquel intervalo en que ninguno de los extremos pertenecen al conjunto que él representa
-intervalo cerrado
Es aquel intervalo en que ambos extremos pertenecen al conjunto que él representa
-intervalo semi cerrado, semi (abierto)
Es cerrado por la izquierda y abierto por la derecha, e incorpora solo al límites "a" entre sus componentes.
Es cerrado por la derecha y abierto por la izquierda, e incorpora solo al límites "b" entre sus componentes.
-intervalos infinitos
En este tipo de intervalos se conoce el límite izquierdo pero no el derecho. Para este tipo de intervalos se pueden dar dos situaciones, que el intervalo sea abierto ó el intervalo sea cerrado en la izquierda, en cuyo caso se representan:
-infinito negativo
En este tipo de intervalos se conoce el límite derecho pero no el izquierdo. Para este tipo de intervalos se pueden dar dos situaciones, que el intervalo sea abierto ó el intervalo sea cerrado en la derecha, en cuyo caso se representan:
II LIMITES
La expresión Lim F(X)=L significa la diferencia entre f(x) y se puede hacer orbital mente pequeña si X esta lo suficientemente cerca de (a).
CALCULO DEL LIMITE POR TABULACIÓN
lim 3x-4
x-3
x
|
2,9
|
2,99
|
2,999
|
3
|
3,001
|
3,01
|
3,1
|
F(x)
|
4,7
|
4,97
|
4,997
|
5
|
5,001
|
5,01
|
5,1
|
-División Sintética
-Limites Trigonométricos

III DERIVADAS
El calculo diferencial se origina con otro grandes problemas ellos son:
1. Problemas de Aceleración
2.Problema de la Velocidad Media
3.Problema de Máximos y Mínimos
4.Problema de la Tangente
PROBLEMAS DE LA TANGENTE
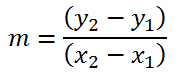


¿Que es una derivada implícita?
Una función está definida explícita mente cuando se da de la forma y = f (x); esto es cuando se da y despejada en términos de x. En cambio, si en una ecuación, como por ejemplo, 2yx = cos3y, existe una función tal que y = f (x), se dice que y es una función que está definida implícitamente por la ecuación. Una ecuación en x e y puede definir a más de una función implícita.
En muchas ocasiones no se puede resolver explícita mente una función dada en forma implícita. Es posible hallar la derivada de una función expresada implícitamente, sin necesidad de transformarla en su equivalente explícita.

Ejemplo 1
Ejemplo 2
Una función está definida explícita mente cuando se da de la forma y = f (x); esto es cuando se da y despejada en términos de x. En cambio, si en una ecuación, como por ejemplo, 2yx = cos3y, existe una función tal que y = f (x), se dice que y es una función que está definida implícitamente por la ecuación. Una ecuación en x e y puede definir a más de una función implícita.
En muchas ocasiones no se puede resolver explícita mente una función dada en forma implícita. Es posible hallar la derivada de una función expresada implícitamente, sin necesidad de transformarla en su equivalente explícita.

Ejemplo 1
Ejemplo 2
DERIVADAS DE FUNCIONES TRIGONOMÉTRICAS



